-





-

Yahtzee








Change to

Yahtzee is a traditional game of chance. Other names of this game are Yam and Yatzy. It is played with five dice. Any number can play and the goal is to get the highest score on a score sheet. You throw the dice, decide which ones to keep and throw the remaining dice again. After the third roll at the latest you decide what box to fill in the score card. There are as many rounds as scoring boxes. If there is no suitable box to fill you will have to put a zero in one of the empty slots. Different versions of the game have different boxes but they all have a box for Yahtzee, getting five of a kind. This is the hardest but most valuable box to fill.
How big is the probability of Yahtzee? That is the question for this project. It is illustrated by the java applet above.
The “Petals” button leads to a quiz called “Petals of the Rose”. Its only relation to the project is that it requires five dice. Roll the dice and guess a number. Push check to check your answer. Repeat until you figure it out.
Back to Yahtzee! The roll and reset buttons rolls and resets the dice. To hold or release a die push the symbol below the die. There are two ways to decide the probability for getting Yahtzee with n throws at your disposal, calculate or simulate. The statistics button does it the Monte Carlo way, simulating 10.000 trials. Dice are rolled and hold until they are all alike. The number of throws needed for Yahtzee is registered and their relative frequencies are shown in a diagram. The relative frequencies seem to approach certain values. The computational task is to calculate these values.
Calculating probabilities for getting Yahtzee might seem like a routine exercise in combinatorics but it can lead to all kinds of interesting stuff. It will involve statistical theory and linear algebra. There are also interesting parallels between Yahtzee probabilities and the theory of quantum mechanics. The navigation bar leads to texts on these subjects. The texts introduces concepts that are applicable to the problem. They are very condensed so If you want to learn more about any of the subjects I would recommend reading an introductory book.
The best option after each throw is to find the number that is most frequent, keep those dice and throw the rest again. If there are more than one number that is most frequent say 2,3,5,5,3 you could of course choose to hold on to either 3’s or 5’s. If they are all different, holding on to one or none is equivalent. The dice can be in one of five different states after each throw.
Ψ1,Ψ2,Ψ3,Ψ4,Ψ5 : The most frequent number occurs 1, 2, 3, 4 or 5 times.
Throw the dice hold on to the most frequent number and throw again. The road to Yahtzee could look like this:
→Ψ2→Ψ2 →Ψ3→Ψ3→Ψ3 →Ψ4→Ψ4→Ψ5
A time series in discrete steps with Ψ(1)=Ψ2, Ψ(2)=Ψ2, Ψ(3)=Ψ3, Ψ(4)=Ψ3, and so on.
Duplicate yourself in a million copies and let all the copies perform the same Yahtzee experiment. At t=1 some of you will be in state Ψ1, others in Ψ2, and a few lucky ones in Ψ5. Seen from above you are in a combination of states:
Ψ(1)= P1Ψ1+ P2Ψ2+ P3Ψ3+ P4Ψ4+ P5Ψ5 Pi is the probability of being in state Ψi
To get the state at t=2 or any later time we need transition probabilities Pji of going from state i to j. If you have two equal dice and throw the other three dice then the probability of getting four equal is given by the conditional probability P42.
Conditional probabilities:
Going from 1 2 3 4 5 from ↓ ↓ ↓ ↓ ↓ To 12345 12345 12345 12345 12345 12345 → 1 P11 P12 P13 P14 P15 12345 → 2 P21 P22 P23 P24 P25 12345 → 3 P31 P32 P33 P34 P35 12345 → 4 P41 P42 P43 P44 P45 12345 → 5 P51 P52 P53 P54 P55 The transition probabilities Pji of going from i to j form a 5 by 5 matrix that operate in a linear space where Ψ1,Ψ2,Ψ3,Ψ4 and Ψ5 form an orthonormal basis. If this sounds like Greek try linearity in the navigation bar. The number of equal dice will never decrease so Pji = 0 if j is less than i. The sum of each column should be one. If we have state Ψi with i equal numbers and throw the rest we will end up in another state Ψ.
Ψi is transformed into Ψ =
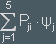
A general state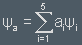 will be transformed into
will be transformed into 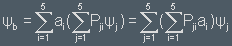
This is a multiplication of the P-matrix with the a-vector. The transformation Ψa → P(Ψa) can be written as a multiplication a → P·a.
The initial state after throwing all five dice is Ψ(1). This vector shows the initial probability distribution. After each round the distribution between states will change as Ψ(n+1) = P∙y(n). After n rounds Ψ(n) = Pn-1∙Ψ(1). A process where the probability distribution changes and the transitions from one step to the next depend only on the previous state, not earlier states and the transition is described by transition probabilities is called a Markov process. Many problems in various fields can be modelled with a Markov process.
The amplitude of the Ψ5-component is the probability of having five equal dice. With these hints it should be possible to calculate the limiting values of the relative frequencies in the statistical simulation above. If you don’t reach the following result then at least one of us will have made an error.
f(n)=1/13·2-5-2n·3-1-3n ·5-1+n·(-539·2n + 13· 33+n·42+n + 455·2n·91+n-9328 ·15n)

