-



-
Quantum mechanics
There are many parallels between the Yahtzee thought experiment and quantum mechanics. When the five dice are thrown in the first round the situation is described by a probability distribution over five possible states:
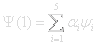
The states Ψi form a base in a 5-dimensional real linear space and Ψ(1) is a vector in this space. Ψ is transformed after each round to a new probability distribution by the transition matrix P.
Ψ(i+1) = P∙Ψ(i)
The probability of being in a state with five equal dice after n rounds equals the Ψ5-component of Ψ(n).
A physical state in quantum mechanics |Ψ> is also described by a vector. This vector belongs to a complex linear space, a Hilbert space. A Hilbert space is a complete inner-product linear space. The inner product or scalar product of a vector space is a function from pairs of vectors to scalars (real or complex), that satisfies:
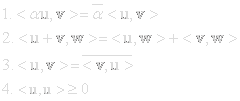
With an inner product in place the length or norm of a vector is defined as:
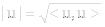
The scalar product in
 3 is defined as:
3 is defined as:<u,v> = |u|∙|v|∙cosθ where |u|=
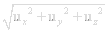 and θ is the angle between
u and v.
and θ is the angle between
u and v.
or
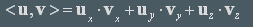
u and v are called orthogonal if <u,v>=0, a generalization of perpendicular. A set of vectors are orthonormal if they are mutually orthogonal and of norm one. A space is complete if every sequence of vanishing separation has a limit point that belongs to the space.

The die-state is a superposition of five basis states Ψi just as a quantum state is a linear combination of states. The quantum state space can be of finite or infinite dimension. The electron’s spin state can be described by a vector |Ψ> = a|Ψ↑> + b|Ψ↓> in a two-dimensional space of spin up and down. A particle confined to movement along a line is described by a complex-valued wave-function Ψ(x) x∈
 .
Ψ(x) belongs to an infinite-dimensional function space spanned by wave
functions Ψn(x)=einx. A particle in three dimensions with a
state that changes in time has a complex valued wave function defined on space-time
.
Ψ(x) belongs to an infinite-dimensional function space spanned by wave
functions Ψn(x)=einx. A particle in three dimensions with a
state that changes in time has a complex valued wave function defined on space-time 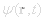 .
.The scalar product is given by :
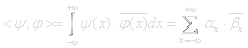
|Ψ(x)|2 is the probability distribution of the particle. Since the particle must be somewhere, integrating |Ψ(x)|2 from −∞ to +∞ gives:
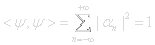
This is similar to the die that has to be in one of five states Ψ1 to Ψ5. The coefficients αi are probabilites that add up to one. The quantum coefficients are complex-valued amplitudes that must be squared |αi|2 before they can add up to one.
The probability distribution of the die evolves in discrete steps through the transition matrix, Ψ(i+1) = PΨ(i). The matrix has columns that add up to one which will keep the total probability equal to one (check this!).
The quantum mechanical evolution of a state from |Ψ(t0)> to |Ψ(t)> is also linear, given by a unitary operator |Ψ(t)> = U(t,t0) |Ψ(t0)>. Unitary matrices satisfy U †∙U=E. The adjoint operator U † is given by interchanging rows and columns and conjugating the elements. Unitary operators conserve the norm <Ψ(t),Ψ(t)> = <Ψ(t)|U †∙U|Ψ(t)> = <Ψ(t0),Ψ(t0)> = 1. The traditional Schrödinger equation is another way to describe the evolution:
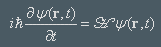
H is the Hamiltonian operator that acts on elements in the Hilbert space, it is related to the unitary operator. An incremental evolution U(t+dt,t) is given by:
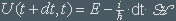
E is the identity operator. The Hamiltonian for a system is constructed by taking the classical energy function of the system and replacing momentum variables with linear operators

A particle in potential well V(x) with classical energy H=p2/2m+V(x) would be described by a wave-function satisfying the Schrödinger differential equation:
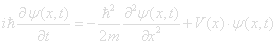
A classical particle is confined to the area with positive kinetic energy. The total energy Etot exceeds the potential energy V(x). Quantum phenomena can be very strange, the wave function Ψ(x) of a quantum particle has a probability distribution |Ψ(x)|2 that extends into the forbidden zone. This makes it possible to tunnel through potential barriers that would stop a classical particle. Quantum tunneling happens every time a radioactive nucleus emits an alpha-particle.
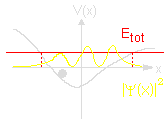
All measurable physical quantities are described by self-adjoint operators O = O†. Self-adjoint operators in a Hilbert space have eigenfunctions O|φn> = λn|φn> that span the space. |φn> represents a state that always result in the value λn when O is measured. Self-adjointness ensures that λn is a non-complex number. An orthonormal set of basis states can be chosen from these eigenfunctions. Every physical state can be expanded as:
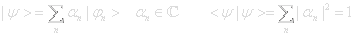
The possible outcomes of measuring O are restricted to the values λn and the probability of getting λn in a state with a serial expansion |Ψ> = Σnαn|φn> is |αn|2. To get the likelihood of λn, project the state |Ψ> onto the basis vector |φn> and square the amplitude.
Back to Yahtzee! We can introduce an inner product in the space by defining <Ψi|Ψj> = δij This makes (Ψ1 , Ψ2 , Ψ3 , Ψ4 , Ψ5 ) an ON-base. Every state can be written as Ψ = ΣαiΨi with Σα=1. Each basis state represents a certain outcome of the observation “maximal number of identical dice”. The difference is that our amplitudes are real numbers that represents probabilities and the quantum amplitudes are complex and must be squared to get probabilities.
A quantum mechanical speciality is the measurement process which represents a reduction of the wave function in a rather mysterious way into one of the allowed eigenstates of the observable being measured. This corresponds in the Yahtzee experiment to the fact that we always observe a definite outcome never a strange probabilistic superposition.
The thought experiment with a large number of parallel dice-throwers represents an all encompassing situation where all outcomes are realized in proportion to their likelihood. This is a parallel to the many worlds interpretation of Q.M. where the wave function never collapses in a measurement process. The world just divides itself into parallel universes where all different outcomes are realized.
There is another parallel with Quantum Mechanics in the Yahtzee probability calculations. The calculations can be described as follows in traditional Q.M notation.
Initial state |Ψ(1)>
Probability of being in state Ψi is given by the projection: <Ψi|Ψ(1)>
Second state |Ψ(2)> = P|Ψ(1)>
Probability of being in state Ψi is given by : <|Ψi|P|Ψ(1)>=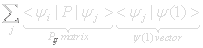
Third state |Ψ(2)> = P2|Ψ(1)>
Probability of state Ψi is : <Ψi|P2|Ψ(1)> =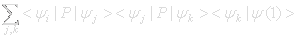
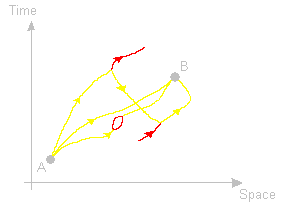
And so on.To calculate the probability of a certain outcome after n throws you sum all possible histories that lead to this outcome. To calculate the probability of Yahtzee in three throws there will be 25 terms. The j,k term in the summation is the probability of the following road to Yahtzee in three steps: →Ψk→Ψj→Ψ5.
This resembles the Feynman path integral formulation of Quantum Field Theory. Q.F.T replaces the classical notion of a single unique history of a system with a sum, technically a functional integral over an infinity of possible histories. The particle paths take place in space-time. Particles travel in both directions in time but particles going backwards in time can be reinterpreted as antiparticles going forward in time. Going from A to B via different particle interaction is represented by different Feynman diagrams that represent quantum amplitudes. They will be added before the absolute is taken and squared. Paths representing different histories seem to coexist and interfere with each other to create physically observable effects on the outcome of a measurement.