-



-
Linear algebra
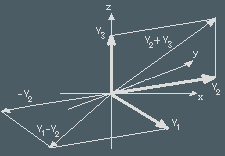
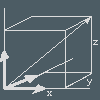
Linear space sounds abstract and mysterious but if you have worked with coordinate systems in two dimensions with x- and y-axis then you have already met one. Add a z-axis and you have a 3-dimensional linear space. Every point P=(x,y,z) can be reached from the origin with a straight line, a vector. Vectors can be added and subtracted as shown. They can be multiplied by numbers. -3.7∙v is a vector in the opposite direction of v but 3.7 times as long.
A linear space over
 (or
(or 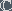 )
consists of vectors that can be added, subtracted and multiplied
with scalars, real (or complex). The formal definition of a linear
space L is:
)
consists of vectors that can be added, subtracted and multiplied
with scalars, real (or complex). The formal definition of a linear
space L is:To each pair of elements u,v in L there is an element u+v belonging to L.
1. u+v=v+u
2. (u+v)+w = u+(v+w)
3. There is an element 0 in L for which u+0= u for all u in L
4. To each u L there is an element u*
L there is an element u* L that satisfies u+u*=0
L that satisfies u+u*=0For each λ

 (or
(or 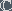 ) and
u
) and
u L there is an element λ∙u in L.
L there is an element λ∙u in L.
1. λ∙(μ∙u) = (λ∙μ)∙u
2. 1∙u = u
3. 0∙u = 0
4. λ∙0 = 0
5. (λ+μ)∙u = λ∙u+μ∙u
6. λ∙(u+v) = λ∙u+λ∙vThe 3-dimensional coordinate system can be generalized to a n-dimensional linear space
 n = { (x1,x2...xn)
| xi
n = { (x1,x2...xn)
| xi
 }. Vectors are represented by n-tuples,
on which operations are defined as follows.
}. Vectors are represented by n-tuples,
on which operations are defined as follows.(x1, x2,...xn) + (y1, y2,...yn) = (x1+y1, x2+y2,...xn+yn)
λ(x1, x2,...xn) = (λ∙x1, λ∙x2,... λ∙xn)The complex space
 n is defined similarly. Check that all axioms
for a linear space are met!
n is defined similarly. Check that all axioms
for a linear space are met!Another linear space over the complex numbers is the space of polynomials with complex coefficients of degree less than or equal to n, Pn ={ Σiaizi | ai

 } with obvious definitions of + and ∙.
} with obvious definitions of + and ∙.A vector in
 3, v=(x,y,z) can be written as
v=x∙ex+y∙ey+z∙ez.
(ex,ey,ez) is a base of
3, v=(x,y,z) can be written as
v=x∙ex+y∙ey+z∙ez.
(ex,ey,ez) is a base of  3.
3.
A base (e1,e2,...,en) in a linear space L is a set of elements in L that :
1. Span the vector space. Every vector can be written as a linear combination v=λ1e1+ λ2e2+...+λnen
2. Are linearly independent. No basis vector can be written as a linear combination of the other basis vectors.Every linear space has a base. There are many ways to choose a base but they all have the same number of elements. This number is called the dimension of the space. Every vector can be written as a linear combination of basis states in a unique way v=λ1e1+λ2e2 +...+λnen.(λ1,λ2 ...λn) are the coordinates of v in the base ei. Another base would give different coordinates but it would still be the same element.
A possible basis in the polynomial space P2 is e1=1, e2=x and e3=x2. The element 3x2+2x+5 has coordinates (5,2,3). The subspace a+bx is spanned by e1 and e2 could be given another base e'1=1+x and e'2=1-x which would alter the coordinates of 3x2+2x+5. The base doesn’t have to be finite. The functional space spanned by einx, n

 and the space of polynomials,
spanned by xn, n
and the space of polynomials,
spanned by xn, n
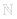 are of infinite
dimension.
are of infinite
dimension.A function, f:A→B takes an element x of set A into an element y=f(x) of set B. f is assumed to be defined for all x
 A but the range can be a subset of B. Functions from
a linear space L to another linear space M with the same scalar field
(
A but the range can be a subset of B. Functions from
a linear space L to another linear space M with the same scalar field
( or
or 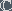 )
that preserve linear structure are called linear transformations.
Preserving linearity means: F(λu+μv) = λF(u)+μF(v) for
all λ,μ
)
that preserve linear structure are called linear transformations.
Preserving linearity means: F(λu+μv) = λF(u)+μF(v) for
all λ,μ (
( or
or 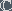 )
)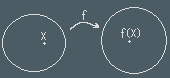
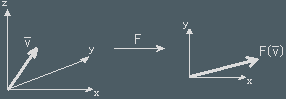
Stretching, scaling and rotations are linear transformations. You can add vectors and rotate their resultant Rot(u+v) or rotate vectors and add the rotated vectors Rot(u)+Rot(v), the result is the same. Translation is not a linear operation since F(0)=0 for every linear operation.
Applying the definition of linearity to a general vector expressed as a linear combination of basis states gives:
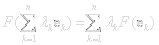
We only need the images of the basis states ek to calculate the function for any vector. Assume F:L→M to be a linear transformation, L a space of dimension A and basis (ei) and M a space of B dimensions and base (fj). The elements F(e1), . . . F(eA) are elements of M with specific coordinates.

This rectangular arrangement of coordinates is called a matrix. a matrix with B rows and A columns is designated as B|A. ajk is the element of row j and column k. The matrix for a rotation α degrees around the z-axis is given by.
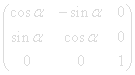
A transformation F with matrix ajk in a certain base will transform a vector into:
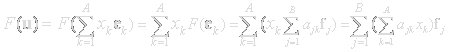
A linear operator from
 A to
A to
 B is given by multiplying an B|A
matrix with an A|1 vector, the result is a B|1 vector. The y-coordinates of F(u)
in base fj are given by multiplying elements from the corresponding row
in the matrix with the x's.
B is given by multiplying an B|A
matrix with an A|1 vector, the result is a B|1 vector. The y-coordinates of F(u)
in base fj are given by multiplying elements from the corresponding row
in the matrix with the x's.
Linear operators and their corresponding matrices can be added and subtracted in a natural way. The matrix A+B corresponds to the transformation FA+GB:x→FA(x)+GB (x). The elements of A+B are aij+bij. Subtraction A-B and multiplication by a scalar λ∙A is defined similarly.
Two linear transformations F:L→M and G:M→N can be combined to a new function H=G°F from L to N defined by H(x)=G(F(x)). This is a natural way to define multiplication of matrices since G(F(x)) is a linear transformation (Show this). The matrix C = B∙A corresponds to the linear transformation GB°FA.
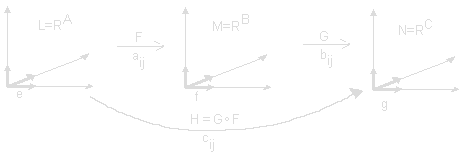
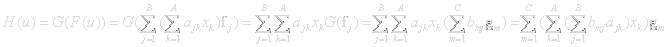
GB°FA is described by a matrix C with elements:
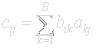
This is the definition of matrix multiplication, C=B∙A. Multiply row i in B with column j in A to get the element cij.
The identity function fE is given by fE(x)=x. The corresponding matrix is called the identity matrix. It has elements Eij = δij. Multiplication with E is easy A∙E = E∙A = A as one would expect from fE°fA=fA°fE = fA. Matrices can be added, subtracted, multiplied and there is an identity matrix. What about division? To divide real numbers you need a inverse y-1 to every number y, x/y = x∙y-1. To get A/B the inverse of B is needed. B-1 must satisfy B-1∙B=E. In linear operator terms this amounts to finding a transformation that for every x sends fB(x) back to x. This can be done if and only if fB is a bijective function. Bijective functions f :A→B never send different vectors to the same image, x≠y f(x)≠f(y) and every point in the value space is the image of some point in
A.
f(x)≠f(y) and every point in the value space is the image of some point in
A.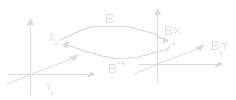
The matrix of a linear transformation depends on the base. The connection between coordinates X and X' of a vector expressed with different base vectors (e1,e2...en) and (e’1,e’2...e’n) are given by a linear transformation that is bijective so T -1 exists.
X = T∙X'
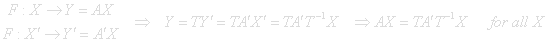
A linear transformation is uniquely determined by its matrix so A and TA’T -1 must be the same matrix, A=TA'T -1. This is very useful if you want to calculate An.
An = (TA'T -1)n = T∙A'n∙T -1
It turns out that for most transformations there is a special base that makes A' diagonal and diagonal matrices are easy to multiply.
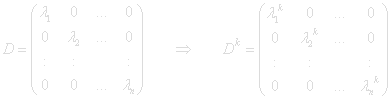
A linear operator that is diagonal in a certain base transforms the basis vectors ei= (0,...1...,0) into parallel vectors λiei
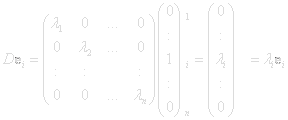
A vector u≠0 that is transformed to a parallel image F(u) =λu is called an eigenvector and λ is the eigenvalue. If a transformation between two n-dimensional spaces has n linearly independent eigenvectors then they can serve as a base that makes the matrix of the transformation diagonal.
The eigenvalues of an operator satisfy Au=λu or (A-λE)u=0 with u≠0. This is a linear equation system with n unknowns. Such a system normally has a unique solution, in this case u=0. Other soluitons exist if A-λE is a non-invertible matrix. There are several criteria for this. Being non-invertible means that the images of the basis vectors do not span the entire
 n-space. This can
be checked by calculating the determinant | A-λE |. The determinant of
A, det(A) measures the n-dimensional volume (with sign) of the base
cube image.
n-space. This can
be checked by calculating the determinant | A-λE |. The determinant of
A, det(A) measures the n-dimensional volume (with sign) of the base
cube image.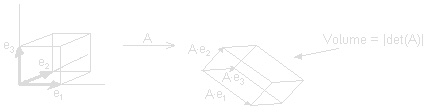
Det(A) is given by a rather complicated formula.
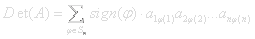
The summation is over all permutations of (1,2,...,n). If n=5 that means 5!=120 terms. The sign of each term is given by the number of transpositions modulo 2 that it takes to make the permutation.
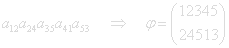
With an odd number of transpositions (35)(24)(12), sign(φ)=−1.
Det(A-λE)=0 is called the secular equation. It is a polynomial equation of degree n. To each eigenvalue λi corresponds an eigenspace of solutions to (A-λiE)u=0. To diagonalize a matrix such as the 5|5 transition probability matrix P. Solve the secular equation and find the eigenvalues λi. Find eigenvectors corresponding to the eigenvalues, construct the base transformation matrix T and its inverse. P is represented by P'=Diag(λ1,λ2,λ3,λ4,λ5) in the new base and P=TP'T -1.