-
-
1. Nonlinear systems 2. One-dimensional maps 3. The logistic map 4. Fractal geometry 5. The Mandelbrot set 6. Multidimensional maps 7. Continuous systems 8. Dissipative systems 9. Conservative systems 
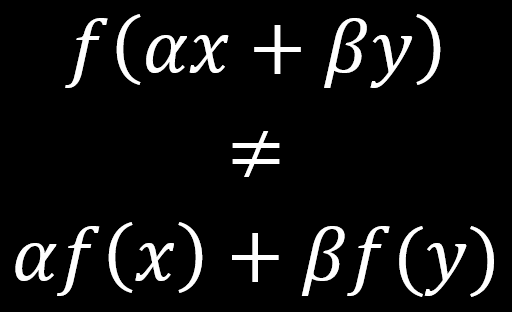
Nonlinear systems
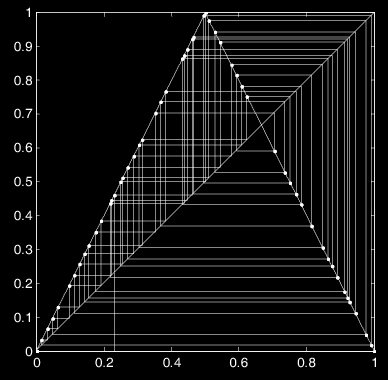
One-dimensional maps
The logistic map
Fractal geometry
The Mandelbrot set
Multi-dimensional maps
Continuous systems
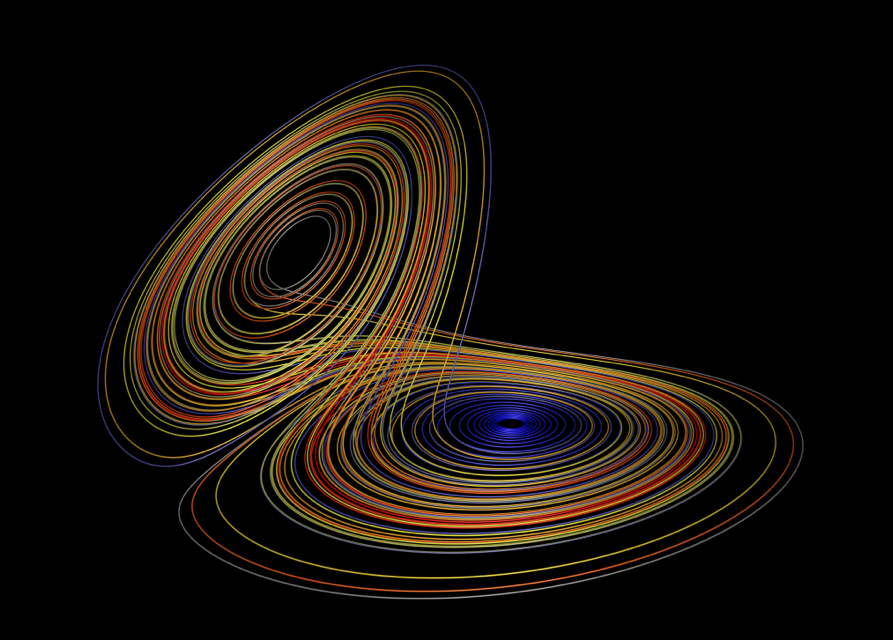
Dissipative systems
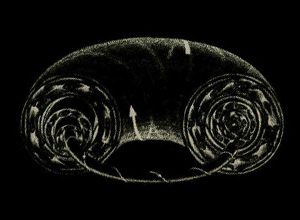
Conservative systems
References
Books [1] Collet P. et al. Iterated Maps on the Interval as Dynamical Systems (1980) [2] Cvitanović P. Universality in Chaos (1989) [3] Devaney R. An Introduction to Chaotic Dynamical systems (1989) [4] Falconer K. The Geometry of Fractal Sets (1985) [5] Falconer K. Fractal Geometry (1990) [6] Finch S. Mathematical constants (2003) [7] Gleick J. Chaos (1987) [8] Mandelbrot B. The Fractal Geometry of Nature (1982) [9] Ohlén G. et al. Chaos (2007) [10] Ott E. Chaos in Dynamical Systems (2002) [11] Peitgen H.-O. et al. The Beauty of Fractals (1986) [12] Peitgen H.-O. et al. Chaos and Fractals (2004) [13] Rasband S. Chaotic Dynamics of Nonlinear Systems (1990) [14] Schuster H. G. Deterministic Chaos (1988) Articles [15] Berliner L.M. Statistics, Probability and Chaos Statistical Science. Vol.7 No.1, 69-90. (1992) [16] Briggs K. A precise calculation of the Feigenbaum constants Mathematics of computation. 57, 435-439. (1991) [17] Derrida B. et al. Iteration of endomorphisms on the real axis and representation of numbers Ann. Inst. Henri Poincaré Vol.29 no.3 305-356 (1978) [18] Derrida B. et al. Universal metric properties of bifurcations of endomorphisms J. Phys A. 12, 269-296. (1979) [19] Feigenbaum M. Quantitative Universality for a Class of Nonlinear Transformations J. Stat Phys. 19, 25-52. (1977) [20] Feigenbaum M. The Universal Metric Properties of Nonlinear Transformations J. Stat Phys. 21, 669-707. (1979) [21] Li T. and Yorke J. Period Three Implies Chaos Am. Math. Monthly 82, 985. (1975) [22] Metropolis N. et al. On Finite Limit Sets for Transformations on the Unit interval J. Combinatorial theory (A). 15, 25-44. (1971) [23] Sarkovskii A. Coexistence of Cycles of a continuous map of a Line into Itself Ukr Mat. Z. 16, 61. (1964) [24] Zeng W.-Z. A. et al. Scaling properties of period-n-tupling sequences in 1D-mappings Commun. in Theor. Physics (China) Vol.3 No.3, 283-295. (1984) Online [25] Boeing G. Chaos theory and the Logistic Map geoffboeing.com/2015/03/chaos-theory-logistic-map/ [26] Burns K. et al. The Sharkovsky Theorem: A Natural direct proof (2008) www.math.arizona.edu/~dwang/BurnsHasselblattRevised-1.pdf [27] Dewaele N. An explanation of period three implies chaos www.siue.edu/~aweyhau/teaching/seniorprojects/dewaele_final.pdf [28] Kartofelev D. Lecture on the logistic map and more www.cs.ioc.ee/~dima/YFX1520/Loeng_11.pdf [29] Leo R. & Yorke J. The graph of the logistic map is a tower (2021) https://arxiv.org/pdf/2008.08338.pdf [30] Wolfram Logistic Map (from Wolfram MathWorld) https://mathworld.wolfram.com/LogisticMap.html [31] Young P.A. The Logistic Map (with Mathematica) physics.ucsc.edu/~peter/242/logistic.pdf